这几天遇到的几个经典电路
这几天在DGJD担任助教,在担任的同时,也见识到了广大学弟学妹们的聪明才智。这几天见到了这么几个看似有些奇怪,其实深含道理的电路。
1.Howland电流源。
2.线性VF转换的实现。
3.线性FV转换的实现。
1.Howland电流源
Howland电流源虽然简单,但是却是这几天我见过的最耐人寻味的电路之一。
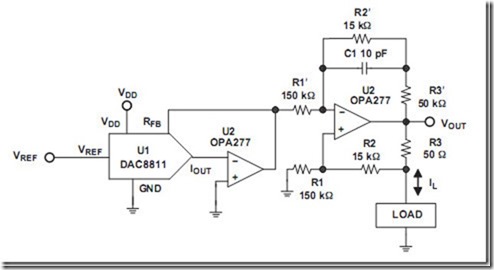
Howland电流源很早之前我就见过,但是当时却不知道这个电压转电流的电路居然还有个名字。最近在DAC8811的数据手册的应用电路部分(数据手册第11页,点击下载),电路图如下所示:
刚拿到这个电路图的时候,我很纳闷。为什么这个电路里面居然把反馈加载了同相端?
假设一种极端情况,在Load负载电阻阻值较大的情况下(即忽略IL):
同相端的反馈为150K/(150K+50+15K)×Vout=91%Vout。
反相端的反馈为150K/(150K+15K+50K)Vout=70%Vout。
也就是说 ,同相端的反馈比反相端的反馈力度还要大。
这么说的话,这种电路,导致放大器工作在比开环更加严重的正反馈的状态下。在这样的情况下,放大器要么满幅输出,要么震荡。
可是作为电流源,这种输出显然不是我们希望的。
就在纳闷之时,一个学弟跑了过来,跟我们说,他看到ADI的一个数据手册上,R3’的值为50欧!
我们恍然大悟:原来TI官方的数据手册也有有误的时候!
如果把R3’改为50欧,那么整个电路就好理解了。
此时,若暂时不关注LOAD,那么同相端以及反相端的电路几乎是一致的。而若考虑LOAD的因素,同相端的反馈则会小于反相端的反馈,运放会工作在线性放大区而非饱和区。
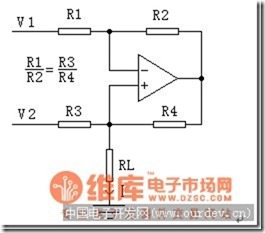
我们把Datasheet中的电路简化,简化成这样一个电路:
假设此时R1、R2、R3、R4之间存在如上图所示的比例,因为放大器工作在线性区,所以同相端反相端的电压应该是相等的,即满足虚短虚断的条件,假设同相端的电压为Vx,运放输出电压为Vo,则存在以下关系:
(V1-Vx)/R1 = (Vx-Vo)/R2
Vx/R3 + Vx/RL = (Vo-Vx)/R4
把1式的Vo解出来,代入2式,并把2式的Vx/R3移到右边,即可得到
因为R1R4=R2R3,所以可得RL上的电流为-V1/R3。
神奇吧,最后得到的RL上的电流,仅与R3和输入电压有关,而且是线性关系。最重要的是,这个电流源不像其他的电流源。因为负载电阻可以直接接地,而且负载电阻上的电流可正可负,具体大小与正负由输入电压来决定。
另外在网上还发现了其他形式的Howland电流源,其原理都一样,形式不同而已:
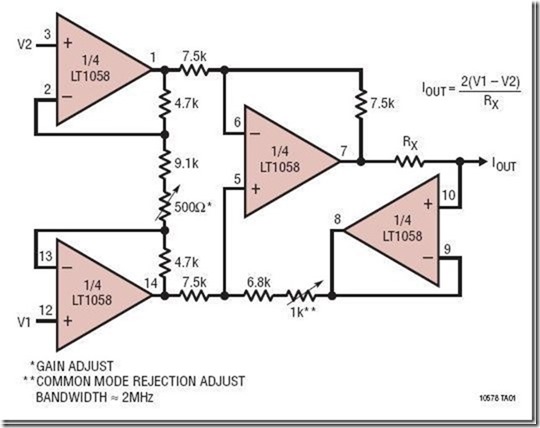
1.一看配色就知道是凌特的电路:
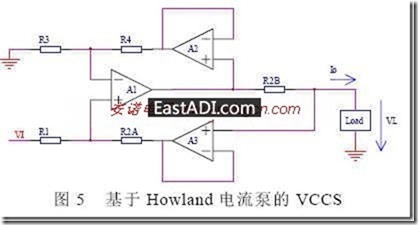
2.中间的Logo烦死个人:
到了现在,再来回想一下为什么反馈要接在同相端:
对于一个接地的负载而言,当电流越大的时候,越需要负载上的电压变大。若将“需要输入电压变大”这个信号量反馈到输入端,那么肯定是要反馈给同相端啦。所以,见到的所有的Howland电流源,应该都在运放的同相端上加了反馈。
2.线性VF转换电路的实现
这周的电子设计竞赛模拟题目中,需要同学实现线性VF转换电路,不得使用现成的VF转换器。也即随着输入电压的线性增大,输出信号的频率也线性增大。
周二的时候,W老师突然打来电话,说这个线性的指标可能做不出来。
顿时我也慌了:明明计算的是可以做出线性来的,为什么W老师又说不可以么?然后就开始分析之。
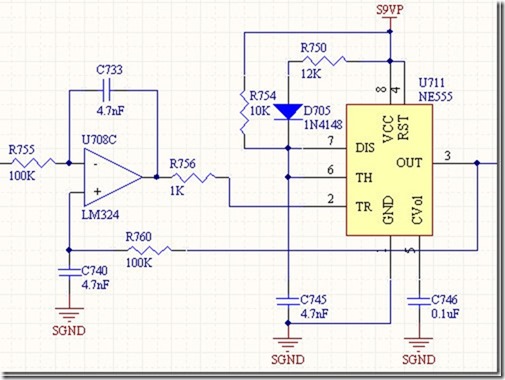
之前设计的一个VF转换电路是采用积分电路+单稳态触发器实现的。电路图如下:
其中运放LM324的供电采用S9VP与SGND。S9VP即正9V,SGND即0V。
原理就是积分电路+单稳态触发器。原理想必我已经不必阐述,在此我主要说下当时是怎么一步一步设计出这个电路的。
1.VF转换器其实就是一个压控振荡器。而普通的压控振荡器通过控制电容充电的截止电平而达到控制振荡器输出频率的目的。而这种振荡器,输入的电压与周期密切相关,在一定的范围内周期跟输入电压成线性关系。
2.但是这种思路设计得到的电路不能满足频率随着输出电压的线性增长。但是却让我们得到了一个重要的关系式:
在一定的范围内,Vi与T成比例增长,即Vi/T=C(C为某一常数)
要实现频率,而不是周期随输入电压线性增长,我们要实现Vi×T=C(C为某一常数)的电路。
3.搜索我们之前遇到的电路,我们很快便知道了,积分电路里面,有:
我们已经看到了Vi×T为一个常数的希望了。若输入信号为阶跃信号,那么就有:
Uo(t)=-Ut/RC
所以,我们下一步的工作就是要为积分器创造一个阶跃的输入信号,并且保证输出Uo到达某一特定电压之后立即停止积分过程。
4.积分电路的输出来控制一个振荡器。而达到一个固定的电压即可触发这种性质,跟单稳态触发器的特性恰好吻合。所以,我们使用单稳态触发器。
5.单稳态触发器的非稳态输出的时间可以调节,但是难以根据输入的频率而自动调节。所以,如果要保证振荡器的占空比恒定为50%是一件很困难的事情。而倘若把非稳态的时间尽可能的缩短,让整个震荡信号输出周期的时间中,非稳态的时间占用小到可以忽略的时候,整个震荡输出的频率就只跟T相关了。
6.振荡器的输出要反馈到积分器中,以给积分器提供一个阶跃输出。而振荡器的方波恰好满足这个要求。我们将单稳态触发器的输出接入积分器的同相端。
7.单稳态触发器的输出接入积分器的同相端,理论上提供了一个阶跃信号,但是却很难保证运放工作在线性放大区。所以我们在反馈上加上电容,防止反馈速度过快。
经过这样的7步考虑,我们最终得到了上面的电路原理图。
3.线性FV转换电路的实现
这周的电子设计竞赛模拟题目不仅要求VF变换是线性的,而且要求FV变换是线性的。
其实按照VF变换的思路来,FV变换达到线性并不难。而可喜的是,发现了一共3种不同的思路的线性FV变换:
1.频率信号-微分电路-单稳态触发器-低通滤波
2.频率信号-微分电路-半波整流-电压跟随-低通滤波
3.频率信号-加1计数器-锁存器-DAC
第一个方案中,输入方波经过微分电路,得到一系列的上脉冲和下脉冲。将这一系列的上下脉冲送入单稳态触发器中。则输入信号频率越高,单位时间内单稳态触发器处于非稳态的时间越长。经过对单稳态触发器的低通滤波,即可得到随输入频率线性增长的输出电压。
第二个方案中,输入方波经过微分电路,得到一系列的上脉冲和下脉冲。一系列脉冲经过半波整流只保留上脉冲。由于每个脉冲的能量是固定的,对上脉冲进行低通滤波之后,频率越高的输入信号,单位时间内将得到更多的脉冲功率,即可得到随输入频率线性增长的输出电压。
第三个方案中,将输入方波送入加一计数器。另外使用一个固定频率(如100Hz)的时钟定时。当到了一定的时间后,将计数器的数值送入锁存器中,并对加一计数器的值进行清零。因为输入信号频率越高,单位时间内计数器累加得到的数值越大,所以把锁存器的值送入DAC即可得到线性增长的电压。
《这几天遇到的几个经典电路》全文完