在上半篇中我们讲了产品的寿命与失效率相关的概念及相互关系。谈起失效率，在生产质量方面也经常提及。产线上也常常说“良率”，其实指的是一回事。与良率一同提及的还有西格玛、Cpk等概念。

四、西格玛（σ）

    西格玛（σ）其实就是标准差。关于西格玛的介绍特别多，这里不再详细展开。我们列出常见的西格玛值及对应的失效率（基于正态分布）：

西格玛	对应的失效率	单位
1	31.731	%
2	4.550	%
3	0.270	%
4	63.342	PPM
5	0.573	PPM
6	0.002	PPM
7	2.560	ppt
8	0.001	ppt

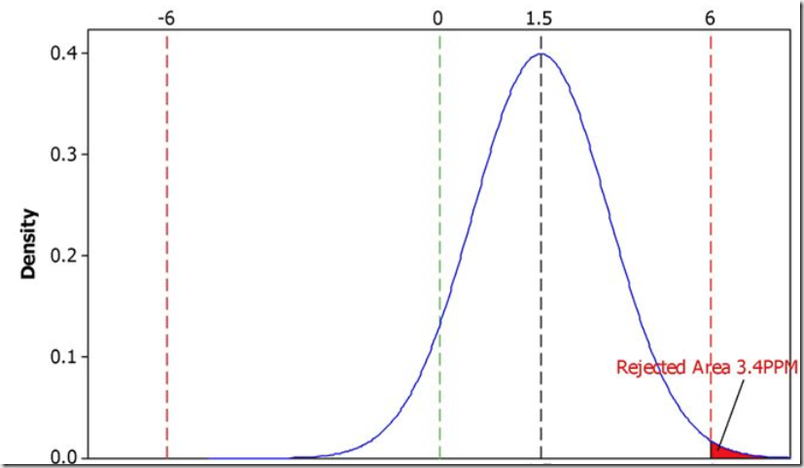
    有一点需要说明的是，大家都在讲的六西格玛，实际上失效率不是上表中的0.002ppm，而是3.4ppm，跟上表的数值相比明显偏大。我也是搞了很久才弄懂为什么。其实上表是在分布的中心值没有偏移的情况下得到的值。当分布的中心值跟规格的中心值相比产生偏差的时候，其失效率的数值就会产生变化。根据摩托罗拉的经验，长期的数据分布跟短期数据分布相比一般会产生1.5σ的偏差。

    最难理解的部分来了。我们说的6σ，其实是指的在中心值已经偏了1.5σ的情况下，我们达到4.5σ就可以了，做到更高的标准对于降低失效率而言没有意义。

    而不能这么理解：6σ是指的我们要达到的标准，如果要满足6σ的要求，在中心值有1.5σ的偏差的情况下，我们要做到7.5σ的标准才能达到6σ的要求。

    所以，在分布产生1.5σ偏移后，分布左侧在-6σ以下的概率就非常小，而分布右侧超出+6σ的概率约为3.4PPM，所以总的失效率为3.4PPM。

五、Cpk

    学过质量管理五大工具（FMEA、APQP、PPAP、SPC、MSA）的人应该知道，SPC里面最重要的概念可能就是Cpk了。学过Cpk的人可能知道Cpk表征了产线的制程能力，体现了制程的稳定性。学过Cpk的人也可能知道Cpk以1.33为界。小于1.33说明制程能力需要加强，大于2说明制程能力过强需要考虑是不是该降低成本了。

    那Cpk到底是什么，我们先从Cpk的计算方法开始。

1. Cpk如何计算

    Cpk的计算方法有两种。

    第一种是先计算Cp 与Ck，再计算Cpk。其中Cp表示可重复性，Ck表示准确度（偏离规格中心的程度）。

Ck = (M-X)/(T/2)，

    其中M为规格中心值，X为量测数据平均值，T为规格宽度。

Cp = T/6σ

    其中T为规格宽度，σ为量测数据的标准偏差。

    最终得到Cpk：

Cpk = (1-Ck) x Cp

    需要注意的是在这种计算方法里面可能会出现负值。如果出现负值需要取绝对值。

    第二种方法是直接计算Cpu与Cpl（距离上下限的差），直接得到Cpk。

Cpu = (USL-X)/3σ

    其中，Cpu为距离上限的差。USL为规格上限，X为量测数据平均值，σ为量测数据的标准偏差

Cpl= (X-LSL)/3σ

    其中，Cpl为距离下限的差。LSL为规格下限，X为量测数据平均值， σ为量测数据的标准偏差。

    Cpk就是两者的最小值。

Cpk = MIN(Cpl, Cpu)

    两种计算方法得到的Cpk的值是一模一样的。因为它们所表征的物理意义是一样的。

2. Cpk的物理意义

    我们在一个线段上把上文中提到的规格中心值、规格宽度、量测数据平均值、规格上限、规格下限标记出来。

    我们把上面方法一提到的Cpk计算公式化简一下，可以得到

Cpk = (T/2+M-X)/(3σ)

    需要注意的是因为在Ck计算中，M-X为负值，所以取了相反数（X-M）之后进行了计算。我们先看分子，T/2就是线段MB，M-X即是线段MB-MX，所以分子表示的是XB的长度。即：

Cpk = XB/3σ

    我们再来看方法二。在方法二中是对Cpu与Cpl取最小值。Cpu的分子为USL-X=XB，Cpl的分子为AX。显然，Cpu比Cpl小。即：

Cpk = XB/3σ

    从物理意义上理解，两种Cpk的计算方法是完全等价的。其数值都等于XB/3σ。观察上面的图不难得知，Cpk的物理意义就是：（在中心值有一定偏差的情况下）允许我们偏差的量跟我们实际产线达到的σ值的比值。分母为3σ是说明我们以3σ为相对标准。

    从这个物理意义，我们可以知道决定一个产线Cpk的因素有两个，一是允许我们偏差的量，二是产线实际的3σ值。允许我们偏差的量由产品中心值偏差与制定的规格大小有关。在定期检查标定的产线中，我们可以认为中心值偏差为0，这个时候允许我们偏差的量完全由制定的规格大小决定。

    假如先不考虑中心值偏差，根据上表，如果我们产线制程能将σ值控制在能达到4σ的要求，那么此时的Cpk就等于4σ/3σ=1.33，对应失效率为63ppm，我们就认为此时产线良率达标。相似的，如果能达到5σ的要求，此时的Cpk就等于1.67；如果能达到6σ的要求，此时的Cpk就等于2。易得到一个结论：Cpk的值等于西格玛值除以3。

    我们只要做到4.5σ就可以达到六西格玛的要求，因此，这个时候对应的Cpk值为1.5。

六、感性认识Cpk、西格玛

    下面列出不同Cpk、西格玛对应的失效率的值，让大家对这些值意味着什么有一个感性的认识。需要说明的是下表是基于正态分布计算出来的值，其失效率的计算公式为ppm = 10^6*(1-NORMDIST(3*Cpk, 0, 1, 1))*2。

Cpk	西格玛	失效率	失效率单位
0	0		百分比
0.02	0.06	95.22	百分比
0.04	0.12	90.45	百分比
0.06	0.18	85.72	百分比
0.08	0.24	81.03	百分比
0.1	0.3	76.42	百分比
0.12	0.36	71.88	百分比
0.14	0.42	67.45	百分比
0.16	0.48	63.12	百分比
0.18	0.54	58.92	百分比
0.2	0.6	54.85	百分比
0.22	0.66	50.93	百分比
0.24	0.72	47.15	百分比
0.26	0.78	43.54	百分比
0.28	0.84	40.09	百分比
0.3	0.9	36.81	百分比
0.32	0.96	33.71	百分比
0.34	1.02	30.77	百分比
0.36	1.08	28.01	百分比
0.38	1.14	25.43	百分比
0.4	1.2	23.01	百分比
0.42	1.26	20.77	百分比
0.44	1.32	18.68	百分比
0.46	1.38	16.76	百分比
0.48	1.44	14.99	百分比
0.5	1.5	13.36	百分比
0.52	1.56	11.88	百分比
0.54	1.62	10.52	百分比
0.56	1.68	9.30	百分比
0.58	1.74	8.19	百分比
0.6	1.8	7.19	百分比
0.62	1.86	6.29	百分比
0.64	1.92	5.49	百分比
0.66	1.98	4.77	百分比
0.68	2.04	4.14	百分比
0.7	2.1	3.57	百分比
0.72	2.16	3.08	百分比
0.74	2.22	2.64	百分比
0.76	2.28	2.26	百分比
0.78	2.34	1.93	百分比
0.8	2.4	1.64	百分比
0.82	2.46	1.39	百分比
0.84	2.52	1.17	百分比
0.86	2.58	0.99	百分比
0.88	2.64	0.83	百分比
0.9	2.7	0.69	百分比
0.92	2.76	0.58	百分比
0.94	2.82	0.48	百分比
0.96	2.88	0.40	百分比
0.98	2.94	0.33	百分比
1	3	0.27	百分比
1.02	3.06	2213.37	ppm
1.04	3.12	1808.51	ppm
1.06	3.18	1472.75	ppm
1.08	3.24	1195.30	ppm
1.1	3.3	966.85	ppm
1.12	3.36	779.42	ppm
1.14	3.42	626.21	ppm
1.16	3.48	501.41	ppm
1.18	3.54	400.13	ppm
1.2	3.6	318.22	ppm
1.22	3.66	252.22	ppm
1.24	3.72	199.22	ppm
1.26	3.78	156.83	ppm
1.28	3.84	123.03	ppm
1.3	3.9	96.19	ppm
1.32	3.96	74.95	ppm
1.34	4.02	58.20	ppm
1.36	4.08	45.04	ppm
1.38	4.14	34.73	ppm
1.4	4.2	26.69	ppm
1.42	4.26	20.44	ppm
1.44	4.32	15.60	ppm
1.46	4.38	11.87	ppm
1.48	4.44	9.00	ppm
1.5	4.5	6.80	ppm
1.52	4.56	5.12	ppm
1.54	4.62	3.84	ppm
1.56	4.68	2.87	ppm
1.58	4.74	2.14	ppm
1.6	4.8	1.59	ppm
1.62	4.86	1.17	ppm
1.64	4.92	0.87	ppm
1.66	4.98	0.64	ppm
1.68	5.04	0.47	ppm
1.7	5.1	0.34	ppm
1.72	5.16	0.25	ppm
1.74	5.22	0.18	ppm
1.76	5.28	0.13	ppm
1.78	5.34	92.95	ppb
1.8	5.4	66.64	ppb
1.82	5.46	47.61	ppb
1.84	5.52	33.90	ppb
1.86	5.58	24.05	ppb
1.88	5.64	17.01	ppb
1.9	5.7	11.98	ppb
1.92	5.76	8.41	ppb
1.94	5.82	5.88	ppb
1.96	5.88	4.10	ppb
1.98	5.94	2.85	ppb
2	6	1.97	ppb
2.02	6.06	1.36	ppb
2.04	6.12	0.94	ppb
2.06	6.18	0.64	ppb
2.08	6.24	0.44	ppb
2.1	6.3	0.30	ppb
2.12	6.36	0.20	ppb
2.14	6.42	0.14	ppb
2.16	6.48	91.72	ppt
2.18	6.54	61.52	ppt
2.2	6.6	41.12	ppt
2.22	6.66	27.38	ppt
2.24	6.72	18.17	ppt
2.26	6.78	12.02	ppt
2.28	6.84	7.92	ppt
2.3	6.9	5.20	ppt
2.32	6.96	3.40	ppt
2.34	7.02	2.22	ppt
2.36	7.08	1.44	ppt
2.38	7.14	0.93	ppt
2.4	7.2	0.60	ppt
2.42	7.26	0.39	ppt
2.44	7.32	0.25	ppt
2.46	7.38	0.16	ppt
2.48	7.44	0.10	ppt
2.5	7.5	0.06	ppt

    看到这个表之后可能会有人对Cpk对应的失效率感到吃惊——Cpk为2.5时对应的失效率是10^-14级别，这种失效率非常罕见但为什么在产线中似乎还时不时的遇到？其实读完本文，了解Cpk的物理意义之后，就能明白，Cpk不止反映制程能力，还由制定的规格有关系。这个时候可能不是因为制程太好了，而是因为规格上下限定的太宽了，已经远超六西格玛的标准了。