一文搞清产品寿命、失效率、Cpk等可靠性相关的所有概念【上半篇】
产品的寿命、失效率、Cpk等可靠性相关的概念在很多人心目中很神秘,会感觉它们“不可预测”、“不可复现”、“随机出现”。读完本文之后就会发现,其实没那么难,寿命/失效率这些东西都是相通的。
导航目录
一、寿命
1. MTBF
寿命跟”故障“相对应。提到寿命,绕不开的一个词是MTBF(Mean Time Between Failure,平均故障间隔时间)。网上有些资料是这样对它进行定义的:
在规定条件下和规定的时间内产品的寿命单位总数与故障次数之比。
这个定义窃以为不能说全错,但也不全对。我们进行更加广义的定义,当测试时间拉到无限长,一直测到所有产品的寿命都终结时,”规定的时间内产品的寿命单位总数“就等于所有产品的寿命之和。而”故障次数“就等于待测品总数。所以广义上的理解就是产品的寿命的平均值。只是现实生活中,我们不可能为了测试产品平均寿命而进行近乎无穷长时间的测试(下文会提到为什么测试时间近乎无穷长),上面的定义只是基于现实考虑的妥协与折中,其实是不准确的。
对于MTBF的理解,我们完全可以从字面意思上进行理解。对于一般产品,出了故障之后也不会进行维修,所以”平均故障间隔时间“实际上就等于”平均无故障工作时间“,而平均的无故障工作时间,其实就是所有产品的工作寿命。
值得一提的是,有个概念叫做MTTF(Mean Time To Failure),用来指代本文所说的MTBF会更合适一些。但在产品出了故障也不会进行维修的情况下,MTBF就是MTTF。针对业内的习惯,大家更多的称其为MTBF,因此本文也以MTBF的说法代替MTTF。
MTBF越长,说明在相同的使用时间内发生失效的次数就越小,也就是这个产品在单位时间内发生故障的概率越小。
2. 故障率
提到失效率或者故障率,一个绕不开的词是FIT(Failure In Time,单位时间内的故障次数)。通常由符号λ表示。故障率的大小为时间倒数,使用的单位是109/小时 = 1 FIT(单位时间故障)。网上有资料是这么对它进行定义的:
故障率是一个项目范围内的故障总数除以在规定条件下特定的测量期间内所花費时间单位总数。换言之,1 FIT表示1,000,000,000小时1次故障。
这个定义窃以为不能说全错,但也不全对。我们进行更加广义的定义,当测试时间拉到无限长,一直测到所有产品的寿命都终结时,”故障次数“就等于待测品总数,而”时间单位总数“等于所有产品的寿命之和。很明显,广义上的理解中,故障率就是产品的平均寿命的倒数,即:
MTBF=1/λ
3. 你真的理解了吗?
我们出几个题目。判断以下说法是否正确:
- 如果某个产品在使用10亿小时的时候,发生了1次失效,那我们就称这个产品在该时间段内的失效率是1 FIT。
- 如果某个产品在使用10亿小时的时候,发生了1次失效,那我们可以认为这批产品的失效率是1 FIT。
- 如果某个产品的失效率是1 FIT,那么在使用到10亿小时之后,就一定会损坏。
- 如果某个产品的失效率是1 FIT,那么损坏的时候,一定发生在10亿小时之后。
- 如果某一批产品的失效率是1 FIT,在使用了10亿小时之后,有50%的已经损坏,50%的仍然完好。
- 如果某一批产品的失效率是1 FIT,记录所有产品的失效时间,所有产品的失效发生时的均值是10亿小时。
答案为vxxxxv。其实第一题肯定是有争议的,原因就在于不管是MTBF还是FIT都应该是一个统计意义上的值。而针对单个案例,说某一个特定的物品的MTBF或者FIT,指的就是这个物品的真实寿命/失效率,失去了统计意义。所以针对第一题,我们说这个特定物品的失效率是1 FIT,也无可厚非。
对于后面的几个问题,初学者一定会有异议,没关系,后文中会一一提及到,这里暂时不做更加深入的阐述。
二、失效模型
1. 浴盆曲线
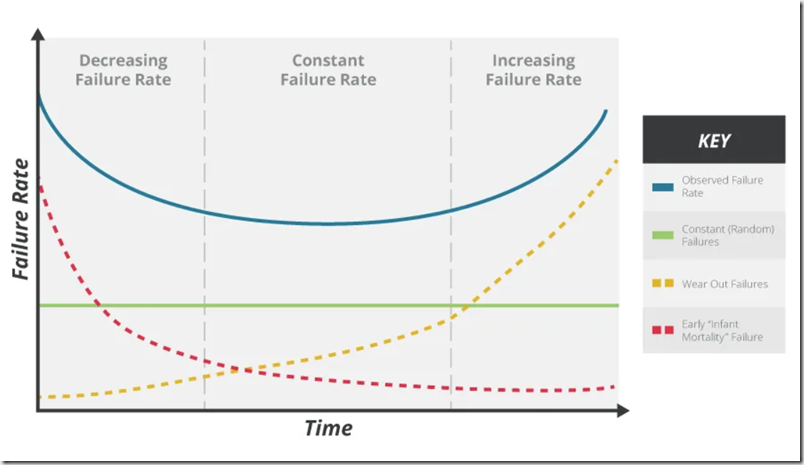
通常在系统的运行寿命中,明显分为三个不同的故障率阶段。下图显示了三个阶段的可靠性浴盆曲线。
第一阶段为早期故障期。第二阶段为偶然故障期。此阶段被假定为产品服务运行阶段。此阶段的故障率预期平稳,因此保持(实际上)恒定。最后一个阶段为磨损故障期。与电子要因相比,在机械要因中此阶段更突出。
早期故障通常是由于发货前检查时未发现的制造误差造成的。各种制造相关的质量保证体系主要是为了尽可能的减少这种故障的发生及流出。在发货给客户之前,如果产品经过了严格的检查和100%筛选测试,确保每个产品都符合规格,那么就可以最大限度的减少早期故障。
对于车载电子产品,电子元器件在出货之前已经经过了老化筛选,早期故障期的元器件已经被最大限度的筛选掉。对于我司,所有前装产品出货前也会100%对整机进行老化测试,确保在整机层面的早期故障期的产品被识别出来。ADAS类的车载电子产品没有机械磨损件,因此磨损故障期可以忽略不计。所以,对于ADAS类的产品,我们可以认为:
对于生产制造执行严格质量管控的前装ADAS产品,失效率分析可以只考虑偶然故障期的随机失效。
2. 随机失效模型
元器件随机失效模型下,每一时刻元器件的失效率是恒定的(参见上图绿色直线)。因此对于一个电子产品,”定期更换新部件“的策略在理论上是没有任何意义的,因为新部件在单位时间内的失效率跟老部件在单位时间内的失效率是完全相等的。
在这样的模型下,一批产品中,如果样本数量足够大,总有一些产品很快就坏了,一些产品寿命趋近于无限长。(这就是前文提到的,为什么测试产品的平均寿命,需要的时间可能接近无限长的原因)
描述元件偶然失效期固定失效率λ下的失效模型为负指数模型:
R(t) = e-λt
其中,R(t)是指可靠性,为0到1之间的值,R(t)=1表示经过时间t后,100%的器件工作正常;R(t)=0表示经过时间t后,100%的器件出现故障。λ 表示失效率,上文中已经提到了它的定义。t表示时间,在可靠性分析中,一般以小时为单位。显然,对于故障率的计算,则为:
Q(t) = 1 – e-λt
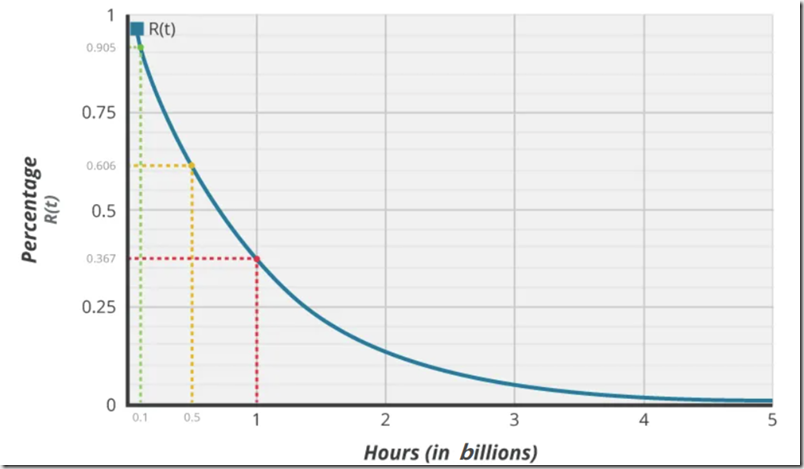
基于这样的模型,我们回到前面的第3-5个问题。如果某一批产品的失效率是1 FIT(MTBF为10亿小时),λ =10–9。我们画出下图的曲线。根据上面的公式,能工作到1亿小时的产品占90.5%,工作到5亿小时的产品占60.6%,真正能工作到10亿小时的产品只占总产品数量的36.7%。这个跟我们的直观感受不太相符,但仔细一想又是很合理的:虽然63.3%的产品寿命不足10亿小时,但36.7%的产品长于10亿小时,有个别的产品寿命还可能远远长于10亿小时,平均下来可能刚好10亿小时。
所以根据这个模型,当一批产品的失效率为1FIT时,所有产品的平均寿命是否刚好是109小时呢?下面我们推导一下。
3. 随机失效模型下的平均寿命
我们先来理清楚我们的问题。
已知:这一批产品的故障率为λ。
求:这一批产品的平均寿命。
平均寿命对于离散型的数据,就是产品寿命总和除以产品数量。但对于非离散型的数据,那就是寿命乘以这个寿命的概率密度,再从0到无穷大做积分。
对于这一批产品中的某一个,如果在时间t的时候刚好坏掉,那就说明产品的寿命是t。其概率密度为:
Q(t)’= [1 – e-λt]’ = λe-λt
所以这一批产品的平均寿命就是:
而1/λ刚好就是MTBF。也就是说,MTBF确实就是这一批所有产品的寿命的平均值。
知道了MTBF、随机失效模型整个的来龙去脉,我们也就明白了几个道理:
- 所有产品的平均寿命就是MTBF的前提条件是随机失效的负指数模型适用,即:不考虑早期故障期,不考虑磨损故障期。
- 1 FIT是指的一批产品的平均寿命是10亿小时,但不能承诺多长时间内100%不会坏。
- 寿命、故障率、多长时间内机器会坏掉多少百分比都是可以互相换算的。
4. 一个系统的FIT值计算
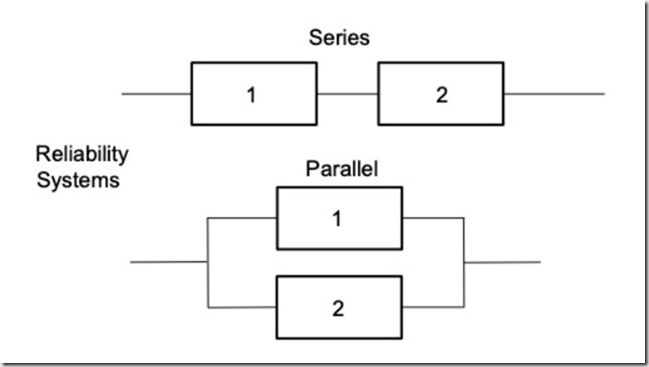
我们先从最简单的系统开始。假设一个系统由两个部分构成:1以及2。那他们之间的关系,要么串联要么并联。串联则意味着任何一个部件失效都会导致整个系统失效。并联意味着两个部件同时失效才会导致整个系统失效。
4.1 串联系统
我们假设部件1、2的可靠率分别为R1、R2,故障率分别为Q1、Q2。则有:
Rs = R1R2
将随机失效模型带入上式中,可得:
Rs = e-λ1te-λ2t = e-(λ1+λ2)t
也就是说,系统的λ=λ1+λ2。在串联系统中,系统的失效率等于各个部件失效率的线性叠加。
4.2 并联系统
我们假设部件1、2的可靠率分别为R1、R2,故障率分别为Q1、Q2。则有:
Rp = 1 – Q1Q2
将随机失效模型带入上式中,可得:
Rp = e-λ1t + e-λ2t – e-(λ1+λ2)t
我们可以看到,系统的λ 不能直接靠简单的加减运算得到,其计算较为繁琐,而且其结果还跟时间有关系。但观察上式可以发现以下要则:
- 因为e-(λ1+λ2)t一定小于e-λ1t ,也一定小于e-λ2t ,所以使用并联系统一定可以使得可靠性提高;
- 若λ1>>λ2,那么最终系统的故障率主要由λ2决定;反之亦然。也就是说,并联系统的失效率主要由系统中最可靠的部件决定。
我们还是希望能给大家一个感性的认识。还是以上问提到的1 FIT的产品为例。假设部件1、2都是1FIT,且使用并联系统,则系统的失效率
Rp = 0.93 FIT(工作100亿小时)
Rp = 0.69 FIT(工作20亿小时)
Rp = 0.51 FIT(工作10亿小时)
Rp = 0.34 FIT(工作5亿小时)
Rp = 0.09 FIT(工作1亿小时)
从上面的数据可以直观看出,在产品生命周期的初期以及中期,并联系统的引入会极大的提升系统的可靠性;但在产品生命周期的末期,并联系统的引入对系统可靠性有一定帮助但作用很小。这一点尤其要注意,假设我们产品本身的FIT值很高,祈望通过冗余来降低故障率的做法是性价比极低的。
功能安全中的“冗余”,即是并联系统。
5. 根据测试数据计算MTBF
上文中已经说明了,不论一个系统的故障率多低,哪怕只有1 FIT,也不能保证在开始使用的前两天就100%不会坏。同理,不论一个系统的故障率多高,哪怕达到1亿FIT,理论上也有个别样品工作1年之后仍然能正常工作。
所以,就个例而言,对10台设备经过了1000个小时的测试之后全都通过了测试,也不能说明MTBF就一定能达到10000小时。但我们知道,“设备全部通过测试”的结果,一定比“其中一台设备异常”的结果要好。从统计学意义上,如果产品失效的统计结果符合某种分布(负指数分布),那我们一定可以统计出在xx%的置信度下,MTBF至少能到多少个小时。
我们把统计学上的数据记在一张表中,便可查表得到根据实验结果计算指定置信区间下的MTBF或者失效率。这里根据JIS5003的标准,我们有:
其中,r为试验期间中的总故障数,ΣT = 总试验期间×试验样本数,k为可靠性等级系数。
k的值可以查下表得到。当r=0时,我们把r当成1进行计算。
| 故障数 | k | |
|---|---|---|
| 信赖度60% | 信赖度90% | |
| 0 | 0.917 | 2.30 |
| 1 | 2.02 | 3.89 |
| 2 | 1.55 | 2.66 |
| 3 | 1.39 | 2.23 |
| 4 | 1.31 | 2.00 |
| 5 | 1.26 | 1.85 |
例如,我们使用77个测试样品进行了1千小时的测试,故障的数量为零。因此可得信赖度为60%的故障率为:
λ = 0.917/77000 = 11909 FIT
FIT值很大。可这个样品本身的失效率非常低,根据以往经验可能只有几个FIT。为了得到这样的测试结果,我们可能需要做 数量×时间 在108级别的大量测试才能得到。怎么通过一些技巧来简化实验呢?
6. 通过加速因子降低测试成本
作用于待测样品上的负荷系数,叫做加速系数。常见的,对于电容,温度、电压都是加速因子。一般的,对于电压,遵循3次方的规律;而对于温度,遵循每10度加速2倍的原则。
假设上面的案例是基于电容,使用125度、75V电压(额定电压1.5倍)得到的测试结果。那我们推测在85度环境中,使用25V的电压,其60%信赖度的故障率为:
亦即此时的λ = 27.6 FIT。相当于MTBF为4141年。
三、感性认识FIT值
下面列出一些FIT值,让大家对这些FIT值意味着什么有一个感性的认识。
| FIT值 | 对应的MTBF年 | 能运行10年概率 | 多少年后坏掉0.3% | 多少年后坏掉10% | 多少年后坏掉一半 |
| 0.1 | 1141552.51 | 99.999% | 3086.360 | 120274.56 | 791263.90 |
| 0.2 | 570776.26 | 99.998% | 1543.180 | 60137.28 | 395631.95 |
| 0.5 | 228310.50 | 99.996% | 617.272 | 24054.91 | 158252.78 |
| 1 | 114155.25 | 99.991% | 308.636 | 12027.46 | 79126.39 |
| 2 | 57077.63 | 99.982% | 154.318 | 6013.73 | 39563.20 |
| 5 | 22831.05 | 99.956% | 61.727 | 2405.49 | 15825.28 |
| 10 | 11415.53 | 99.912% | 30.864 | 1202.75 | 7912.64 |
| 20 | 5707.76 | 99.825% | 15.432 | 601.37 | 3956.32 |
| 50 | 2283.11 | 99.563% | 6.173 | 240.55 | 1582.53 |
| 100 | 1141.55 | 99.128% | 3.086 | 120.27 | 791.26 |
| 200 | 570.78 | 98.263% | 1.543 | 60.14 | 395.63 |
| 500 | 228.31 | 95.715% | 0.617 | 24.05 | 158.25 |
| 1000 | 114.16 | 91.613% | 0.309 | 12.03 | 79.13 |
| 2000 | 57.08 | 83.929% | 0.154 | 6.01 | 39.56 |
| 5000 | 22.83 | 64.533% | 0.062 | 2.41 | 15.83 |
| 10000 | 11.42 | 41.645% | 0.031 | 1.20 | 7.91 |
| 20000 | 5.71 | 17.343% | 0.015 | 0.60 | 3.96 |
| 50000 | 2.28 | 1.253% | 0.006 | 0.24 | 1.58 |
| 100000 | 1.14 | 0.016% | 0.003 | 0.12 | 0.79 |
附录
回到开头的几个问题,我们来揭晓每道题答案是什么。
- 如果某个产品在使用10亿小时的时候,发生了1次失效,那我们就称这个产品在该时间段内的失效率是1 FIT。
(可以认为是正确,但这种说法本身是没有意义的) - 如果某个产品在使用10亿小时的时候,发生了1次失效,那我们可以认为这批产品的失效率是1 FIT。
(信赖度为60%的情况下,失效率为2.02FIT,信赖度为90%的情况下,失效率为3.89FIT,不是1FIT) - 如果某个产品的失效率是1 FIT,那么在使用到10亿小时之后,就一定会损坏。
(上文做过多次分析,不一定) - 如果某个产品的失效率是1 FIT,那么损坏的时候,一定发生在10亿小时之后。
(上文做过多次分析,不一定) - 如果某一批产品的失效率是1 FIT,在使用了10亿小时之后,有50%的已经损坏,50%的仍然完好。
(上文做过分析,概率上讲,会有63.6%已损坏,36.7%仍然完好) - 如果某一批产品的失效率是1 FIT,记录所有产品的失效时间,所有产品的失效发生时的均值是10亿小时。
(正确,上文已经给出了证明)
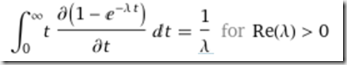
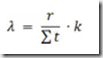

感谢!讲解的通俗易懂。最后的图表感性认识真的很震撼
有人计算过最后那个表么,坏掉0.3%那一列是算错了,其他的是对的
真的吗,我把计算的原始表格上传到这里:http://img.liuwenhao.ink/shared/fit-calc.xlsx
方不方便看下表格里面的计算公式哪里有问题?
谢谢了。
查看了,公式没有问题的,但是公式里面计算的是失效0.27%而不是0.3% (=-LN(0.9973)/0.00000876/A2)
哦哦,那就明白了,0.27%其实是按照3sigma来算的,0.3%是粗略一点的,0.27%更精确一点。